Double Dual Space: An Exercise in Abstraction

One important skill in higher math is being able to recognize a mathematical structure or pattern and abstract it away so that you can apply in to distinct mathematical objects: objects that may at first seem quite different in nature, but that under this new perspective behave similarly if not the identically. This ability to distill the essentials of a problem and relate it to others is central to mathematical problem-solving and in this article I want to go through an example that challenged me when I was trying to build an intuition of abstract vector spaces.

If you don’t already have an understanding of what an abstract vector space is I would suggest checking out an article that I wrote earlier, or any of the numerous sources online. But to make it short and sweet (and to skip a lot), a vector space is a mathematical object that is closed under addition and scalar multiplication, and defined over a specified field F. Meaning that if you take two vectors (defined to be the objects in said vector space) and add them together, or multiply them with a scalar from a specified field, the result will also be in that vector space. There are also other requirements such as that there must be an identity and inverse elements for each of these operations and that these operations must ‘play nicely together’, but I encourage you to review that on your own. For the purpose of this article I will use denote a vector space as V, and we assume that all vector spaces are defined over the same field F.

Dual Space

Our first stop on our journey to understanding the double dual space is another space: the dual space. The dual space of a vector space V, denoted V*, is the set of all linear maps ψ: V → F . These linear maps are special because their codomain is a field (the same field that V is defined on) as such they have some special names including linear functionals, covectors, one-forms and others.

To give a few examples:

• Let V = Rⁿ (over the real field). The dual space is the set of all functions that take a vector in Rⁿ a return a scalar in R. For n=3 an example of a element of V* is T(x,y,z) = x + y + z
• Let V = M(nxn). Then one V* is the set of all functions that take in scalars and return a real number. Examples of these functions are the Trace(M) and det(M) functions.

It turns out that the dual space, which is built on some arbitrary vector space V, is a vector space in its own right. You should prove this to yourself.

• Is it close under additional and scalar multiplication?
• What is the identity element for both operations?

etc.

Now that you have convinced yourself that the dual space is in fact a vector space, you may see where we are going. What’s to stop us from looking at the dual space of the dual space? Or the dual space of that?

The Double Dual Space

To recap, the dual space is defined on a vector space V, defined on a field F, to be the set of all functions that take vectors in V and spit out scalars in F. You can think of these dual vectors as ‘measurement’ vectors, as when we make a measurement, the result is a scalar. ie a temperature/charge/mass distribution etc. So the dual space, in a way, is the space of ‘rulers’.

So what does it mean to define a dual space on top of this dual space? Well we call this new space the double dual space and denote it V**. It is also defined over the same field F, as it ‘inherits’ it from V* which inherits it from V. We already know that this space is a vector space because it can inherit same argument for the dual space.

Using the same definition of the dual space from earlier, we recognize the V** is the set of all functions that take elements of V* to F:

Φ: V* → F.

This means that the double dual space is the set of all functions that take in a linear functionals and spit out a scalar in F. Or, to put it another way, V** is the set of all functions that take in functions that return a scalar and spite out scalars. Pause to let that tongue twister sink in.

So what do these functions look like?

Let’s take a classic example which we will call the evaluation function E_n, for some n, defined over some vectors space V. . We know from above that E_n must take linear functionals in V* to F. Lets define E_0 to be the following:

E_n: V* → F.

v → v(n)

So what does this mean? The first line says that E_n takes elements of V* to the field F, and the second line defines the actual rule. And the rule is evaluation at n! Yes, E_n takes in a linear functional, a function, and just evaluates it at the value n. Since linear functionals return map to F, this must also map to F.

For the sake of example let’s take n to be 0, and V to be Rⁿ. An element of V** could be the function that takes in a linear functional and evaluates it with all of its inputs equal to zero.

The fact that the double dual space is also a vector space, falls out of the proof of a dual space (since it is just the dual space of another vector space).

Canonical Isomorphism Between V and V** and Intuition as V* being a Space of ‘Rulers’

But the example above drops an isomorphism between V and V** right into our lap, namely the function that maps a vector in V, to the double dual vector that evaluates all dual vectors at v. Let me repeat that. The isomorphism maps a given vector v in V, to the double dual vector in V** that evaluates all linear functionals at v.

More formally:

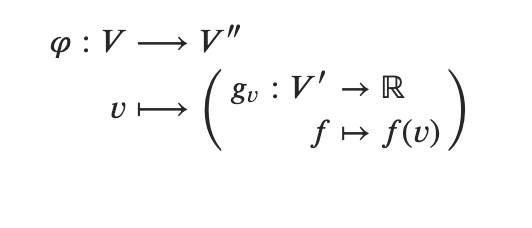
Again, the isomorphism ψ, take some vector v and associates it with E_v: a double dual vector that take linear functionals and evaluates them at v. This may seem confusing at first but after you mull over it for a bit you will realize that the association is almost trivial, natural some might say. It doesn’t depend on any choice of basis, of any choice at all, just the definition of a dual.

Another way to understand this, harkening back to our understanding of the dual space as the space of ‘rulers’ is that there is not a canonical isomorphism between V and V* because there is no natural or obvious way to measure things. Any measurement can be scaled and there is not an obvious answer as to which scaling is the best. On the other hand we can think of the double dual space as the objects that measure the rulers so-to-speak. Here there is a natural way to measure how well these objects are measuring. Namely, measure them on how well they do their job at measuring the things they are suppose to measure.

Notes

If this seems confusing at first, that’s because it is. Sit on these ideas, and come back to them. The objective of this article was to introduce you to beautiful, but often seemingly obfuscating, art of abstraction.

*I accredit idea of the dual space as the space of rulers to this stack exchange answer: https://math.stackexchange.com/questions/3749/why-do-we-care-about-dual-spaces